The appearance of Nozelesn on your computer is a sign that your system’s security has been breached and now the privacy and security of your sensitive data is under threat. Although this infection is highly dangerous for your computer, you can get rid of Nozelesn ransomware permanently. Therefore, in this removal guide we will explain in detail how to remove Nozelesn ransomware from your computer without using any removal program.

What is Nozelesn?
Nozelesn is a ransomware which acts as a file-locker so that it can extort money from its victims. The first appearance of Nozelesn was recorded in July 2018 and since then it has been designated as a malware threat. This infection encrypts the data of its victims and demands money in Bitcoin to unlock that data. Users whose highly sensitive data is locked sometimes pay that money, but those who don’t pay, they end-up losing their valuable data. Therefore, you must uninstall Nozelesn ransomware from your computer the moment you detect its presence.
How Nozelesn Ransomware Entered Your Computer?
The Nozelesn ransomware is distributed through phishing campaigns, which are popularly known as ‘spearphising’. Usually, this malware is attached with an email and when victims click the infected links they end-up installing this ransomware on their computer. Most commonly, this infection uses fake DHL emails to induce victims into opening the email and then clicking the email attachment. If you have become a victim of this malware, then don’t worry and follow the removal steps given below to completely eliminate Nozelesn ransomware from your computer.
How to Avoid Entry of Nozelesn Ransomware?
As described above you will get this infection most probably from phishing emails. Therefore, you can avoid the entry of Nozelesn by taking some simple precautions. Firstly, you should never open emails which are from unexpected sources. Always study the email content carefully before clicking any of its attachments. Also, avoid emails which make tall claims and offers. Install a reputed cybersecurity suite on your computer which can detect and eliminate all phishing emails. Keep an anti-malware program on your computer so that it can detect the entry of such infections at the earliest.
How to Remove Nozelesn Ransomware?
In order to fully remove Nozelesn Ransomware from your computer we have prepared a removal method which uses a four step process.
- Enter Safe Mode with Networking
- Close Suspicious Applications
- Check Start-up Programs
- Delete Ransomware Files Manually
We are describing the removal process for Windows 10 OS, but you can follow the same steps with relevant alterations for other Windows OS as well.
1) Enter Safe Mode with Networking
First you will have to start your computer in Safe Mode as rest of the steps must be executed in that mode.
- Right click on ‘Start’ button and choose ‘Settings’ from the options.
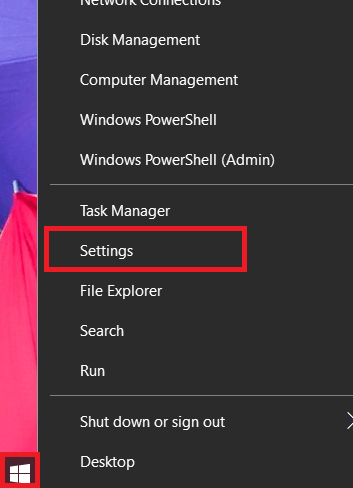
- In the Settings page, select ‘Updates & Security’ option.
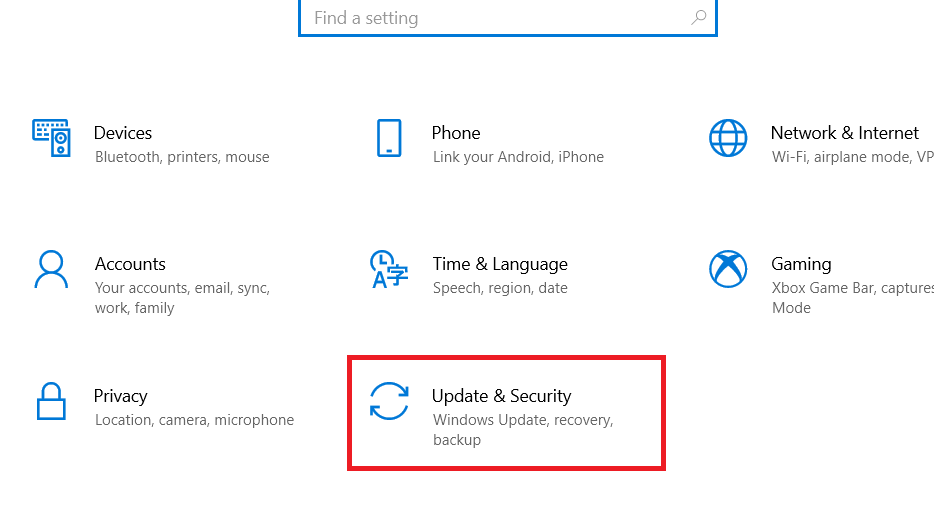
- In Update & Security, select ‘Recovery’ option and choose ‘Restart now’ button.
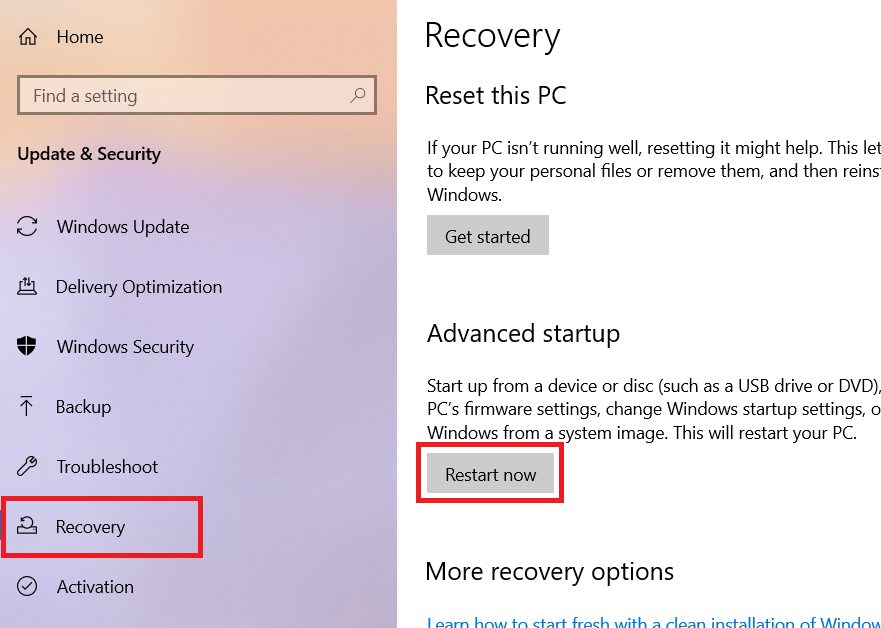
- Windows will begin the restart process, choose ‘Troubleshoot’ option.
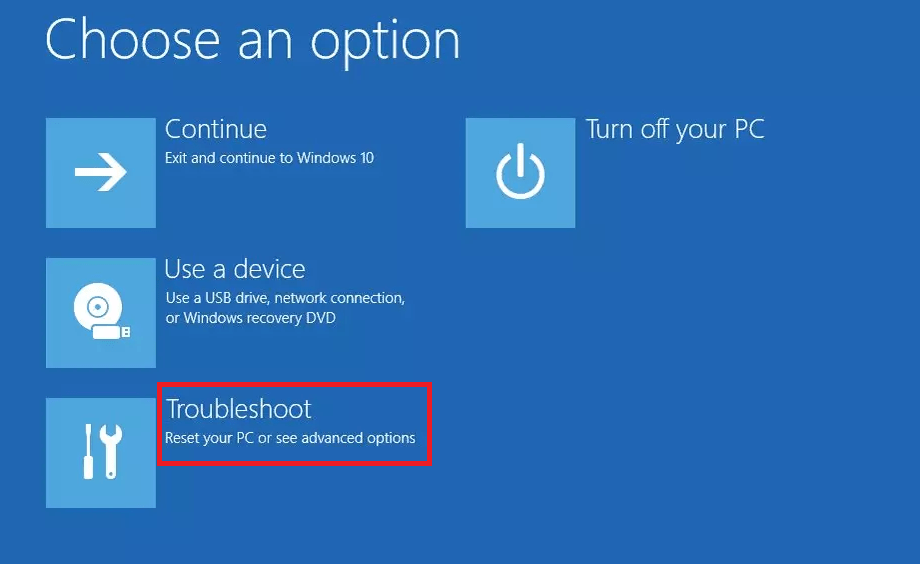
- Choose ‘Advanced options’ button.
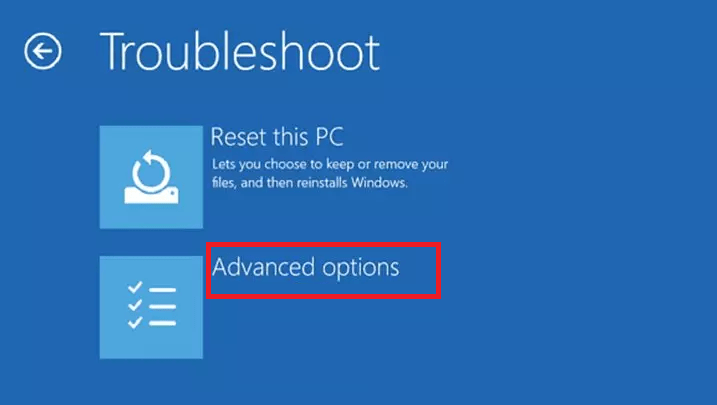
- Choose ‘Startup Settings’ from the available options.
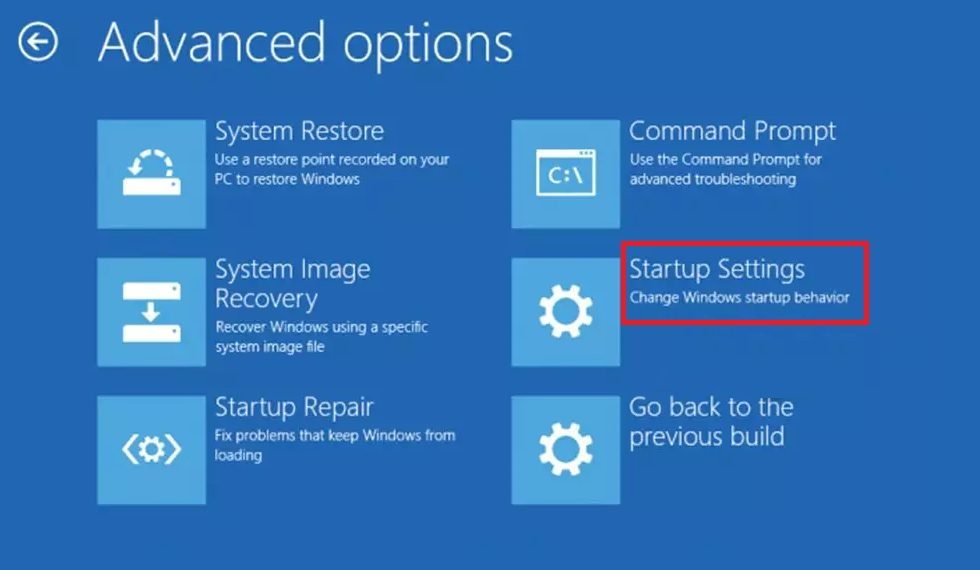
- Click on ‘Restart’ button.
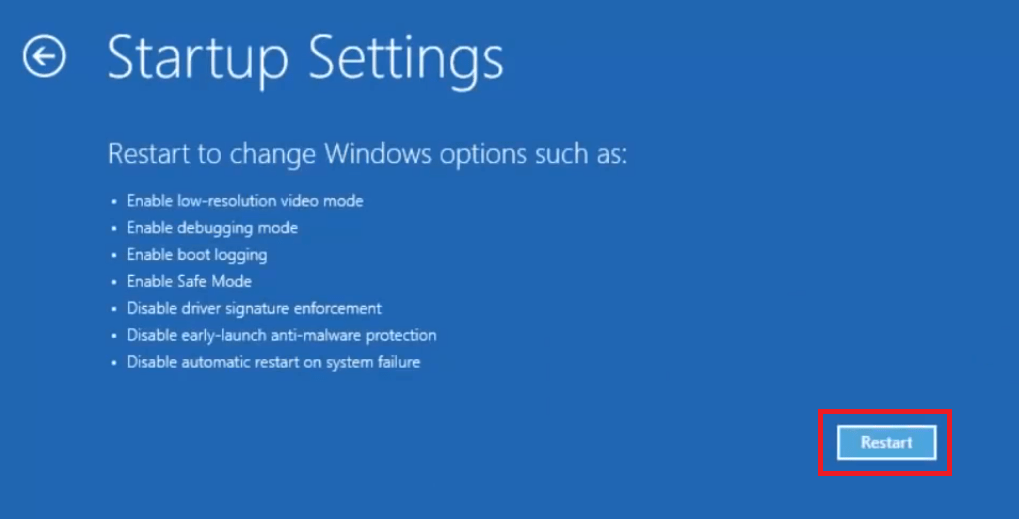
- Press ‘5’ on your keyboard to choose ‘Enable Safe Mode with Networking’ option.

- Wait for your computer to restart, then move to the next step.
2) Close Suspicious Applications
This is the most important step as you will shut down suspicious programs on your computer. Carefully, choose each program. If you make any mistake in this step, then this ransomware might reappear on your computer.
In our examples, we have chosen generic Windows programs, but you must choose the programs which you find suspicious.
- Right click ‘Start’ button and choose ‘Task Manager’.
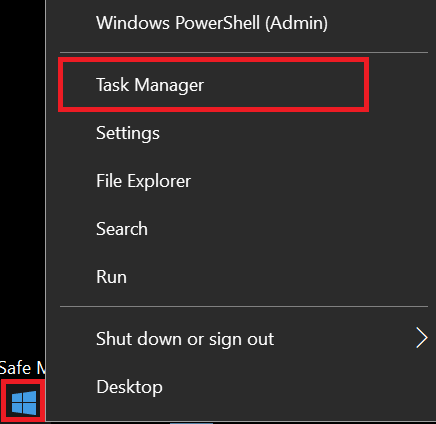
- In the Task Manager, click on ‘More details’ option.

- Under ‘Background processes’, locate a suspicious program, right click it and choose ‘Open file location’. This will open the folder from where the suspicious program is running.
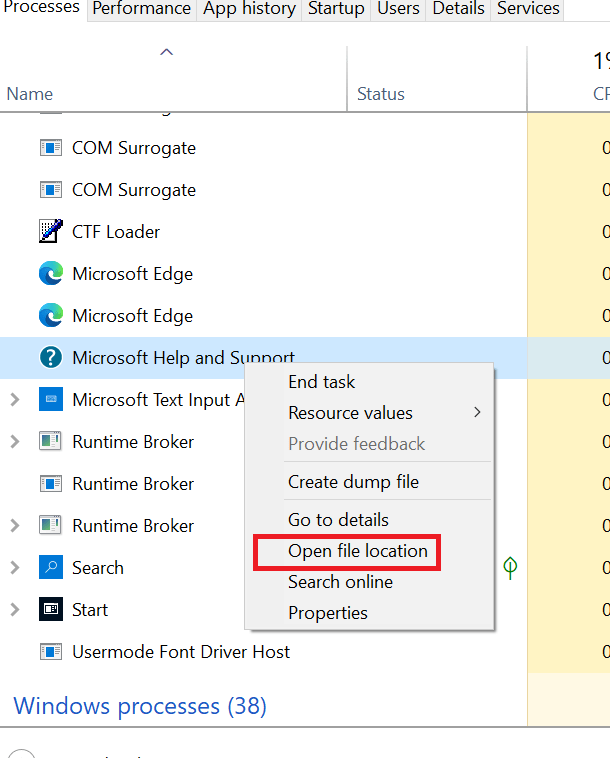
- Now, again right click the same program and choose ‘End task’ to shut down the program.
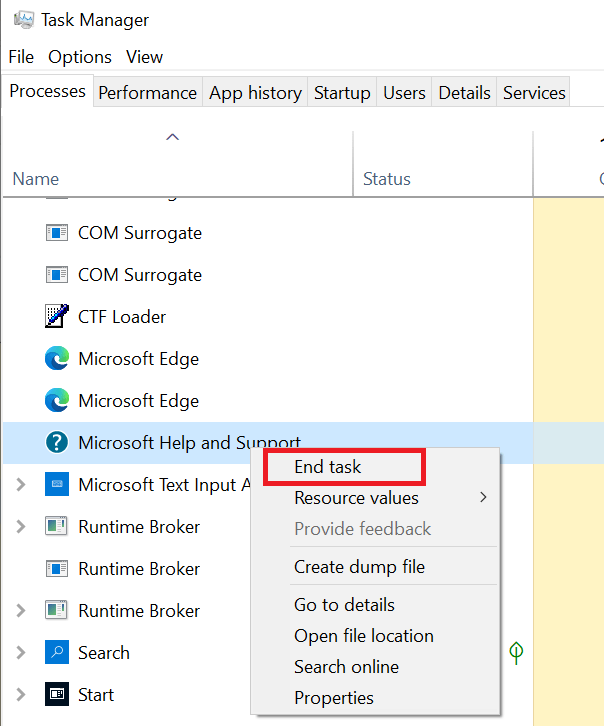
- Next, go to the program folder of Step 3 and delete all its files and folder.
- Repeat these steps for all the suspicious programs you find in Background processes.
3) Check Start-up Programs
Now that you have removed suspicious programs. You should disable them from running during Windows boot-up process.
- Right click ‘Start’ button and select ‘Task Manager’.

- In the Task Manager, click on ‘Startup’ tab.
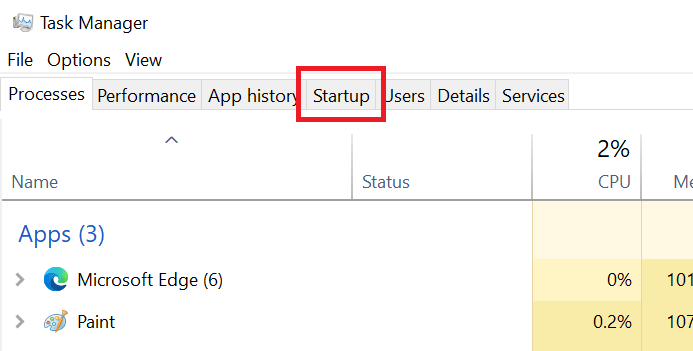
- In the list of programs, locate and right click suspicious program and choose ‘Disable’.
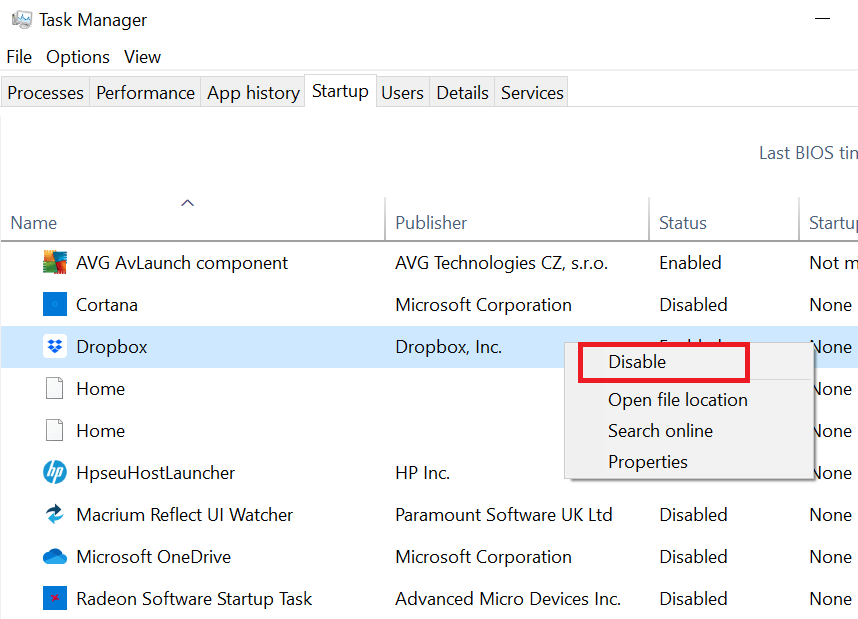
- Follow the above step for all suspicious programs in the Startup list.
4) Delete Ransomware Files Manually
Now you should remove ransomware files manually so that they are completely and permanently removed from your computer.
- Search ‘disk’ and choose ‘Disk Cleanup’ app from the search results.
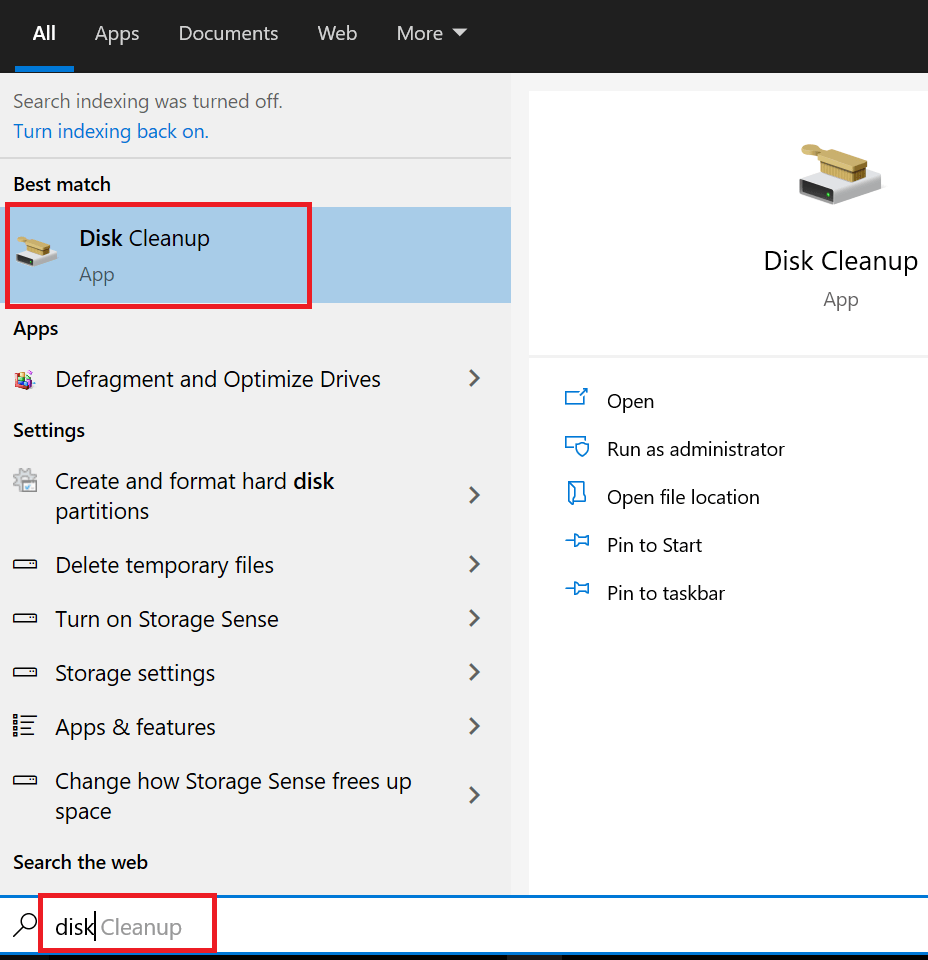
- Choose the driver you want to clean. Mostly, such files are stored in ‘C:’ drive, then click ‘OK’ button.
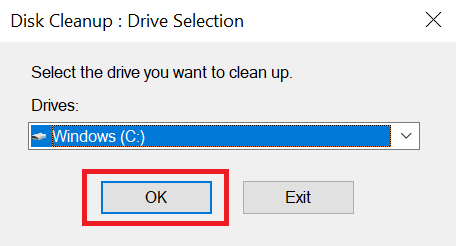
- Wait for the Disk Cleanup utility to scan for the unnecessary files.
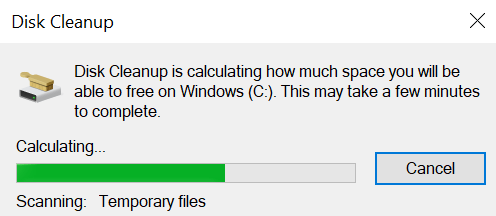
- Choose ‘Temporary Internet Files’, ‘Downloads files’, ‘Recycle Bin’ and ‘Temporary files’ from the list. You can choose any other option as well, but the above mentioned must be selected. Then, press ‘OK’ button.
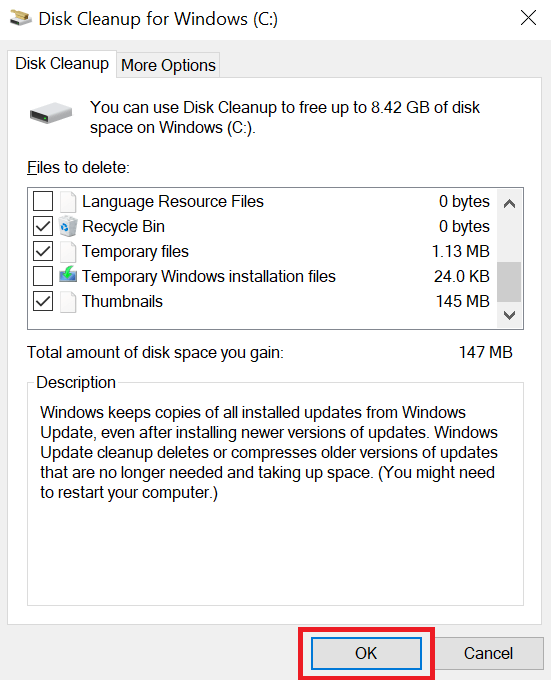
- Choose ‘Delete Files’ in the pop-up message box.
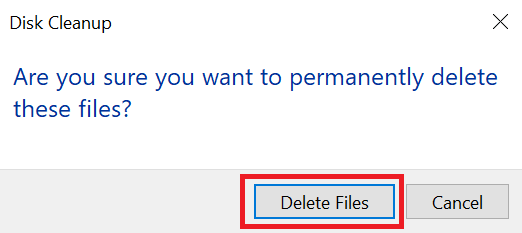
- Wait for the files to be deleted.
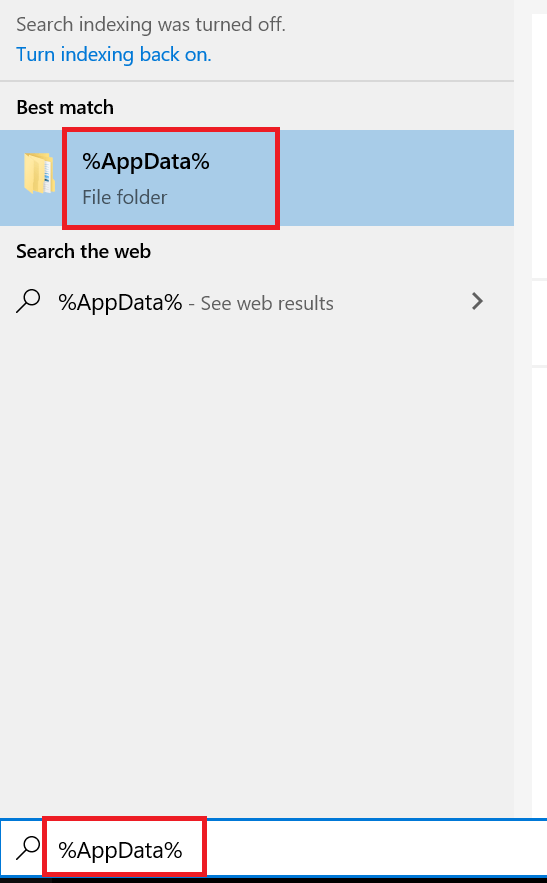
- Once the files are deleted, search ‘%AppData%’ and click on ‘%AppData%’ to open that folder. Then, delete all the suspicious folders inside the %AppData% folder.
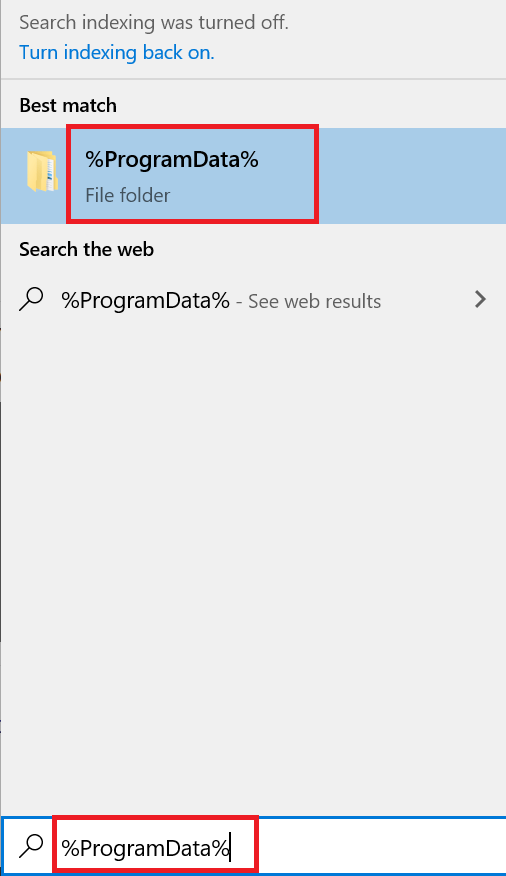
- Next, search ‘%ProgramData %’ and click on ‘%ProgramData %’ to open that folder. Now, delete all the suspicious folders inside the % ProgramData % folder.
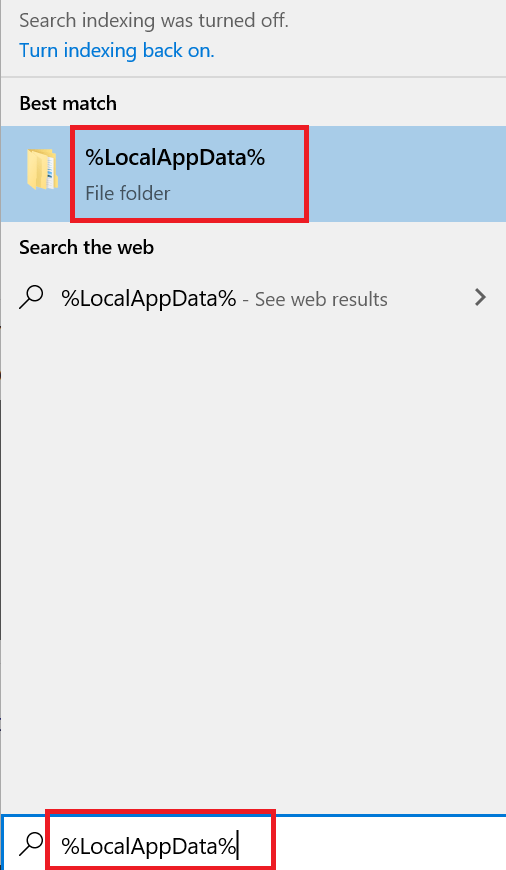
- Now in the search box type, ‘%LocalAppData%’ and choose ‘%LocalAppData%’ folder from the results. Then, delete all the suspicious folders inside the % LocalAppData% folder.
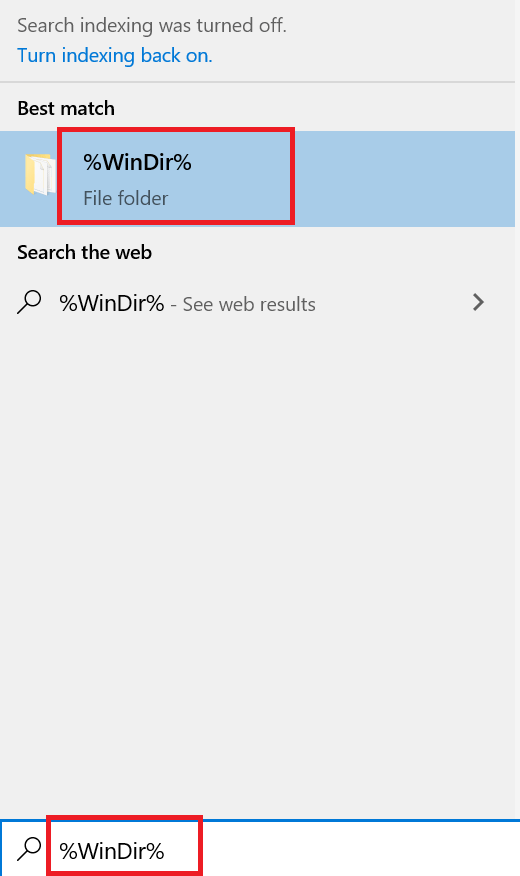
- Finally, type ‘%WinDir%’ in the search box and select ‘%WinDir%’ folder. Next, delete all the suspicious folders inside % ProgramData % folder.
Once you have completed all the above steps restart your computer in normal mode. If you have chosen the suspicious programs correctly, then Nozelesn Ransomware will be completely removed from your computer. Otherwise, you can follow the complete removal process again.
Conclusion
The removal process for Nozelesn ransomware may seem complicated, but it needs to be executed completely if you want desired results. However, if you have lost your data due to this ransomware, then you will have to use some data recovery program to get it back.
